好题“抱团”方能“去难”
无锡市张泾中学 庄佳红
【摘要】
很多时候我们不应仅限于就题论题，而要对试题进行适当的变式，让好题也能“抱团”呈现，将一道静态、封闭的试题从不同的角度、不同的层次、不同的侧面出发，变化为一道动态的、开放的试题，才能让学生排除万难而“取暖”。
【关键词】变式 抱团 一题多变
在寒冬的时候，如果能有多人一起抱团取暖会好过一个人的单独取暖，因为可以积聚力量，增加信心。在我们的数学教学中为了有效达成三维目标，把握好知识容量和思维容量的“度”,处理好教师的点拨与学生思考的关系是非常重要的。所以很多时候我们不应仅限于就题论题，而要对试题进行适当的变式，让好题也能“抱团”呈现，将一道静态、封闭的试题从不同的角度、不同的层次、不同的侧面出发，变化为一道动态的、开放的试题，才能让学生排除万难而“取暖”。下面就谈谈本人在教学中进行的一些实践与思考。
一、课堂实践
（一）一题多解，拓展思维新天地
一题多解主要指在对题目进行多角度、多侧面分析的前提下，通过对题目中的条件和学过的概念、原理进行不同的组合和建模，从而找出多种不同的解题方法。这种训练方法所蕴含的信息量特别大，学生对该方法的掌握能加深对所学知识点的系统性的理解。
例1：如图1，在矩形ABCD中，AB=3，AD=4，P是AD上一动点，PE⊥AC于E，PF⊥BD于F，则PE+PF= .
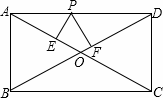
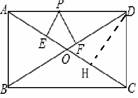
图1 图2 图3
由于这是一道填空题，不必体现详细的解题过程，所以课堂中学生用了多种方式解决，正所谓“众人拾柴火焰高”。
解法一：特殊点法。当P运动到AD的中点时，由全等知PE=PF，故只需求PE的长。易证△AEP∽△ADC
解法二：极端值法。如图2，过D作DH⊥于AC，由勾股定理知道，AC=5，可以把P点向D运动，此时PE不断增大，而PF逐渐减小，当P与D重合时，PF=0，PE就与DH重合，所以只需求DH的长即可。由等积变形：
，
解法三：相似三角形法。由解法一，有学生就会联想，既然有△AEP∽△ADC，那自然有△DFP∽△DAB，那样就会有两个比例式，于是就有了：
两式相加得：
，所以PE+PF=
解法四：面积法。由垂线段联想到高，联想到面积。如图3，连结OP，
△AOP与△DOP的面积之和是3，
通过多种方法，学生对此图印象深刻，于是提炼精髓：“等腰三角形底边上的任一点到两腰的距离之和等于一腰上的高。”运用这一题的方法、基本图形和结论，学生可以解决很多类似问题。
（二）一法多用，形成思维新提升
一法多用指一种解题思路或方法能够解决多个同类型的题目，学生对该方法的熟练掌握，能促使学生建立认知体系，从而做到触类旁通，举一反三。
例2: 下列各图中求∠A+∠B+∠C+∠D+∠E的和.
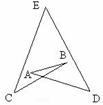
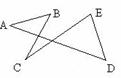
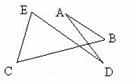
实际上像上面这种问题，可以变化出无数种类似的图，要求这所有角的和，我们可以用一个图形就能完胜，那就是“8”字形。当我们遇到求多个角的和（或差）时，根据图形的特点，适当的添加辅助线构造“8”字模型，然后将求多角的和（或差）的问题转化为求三角形内角和问题。
（三）一题多变，展现思维新视角
一题多变就是对原题适当地进行变化问题或要求，学生通过一题多练，深化对数学概念、规律的理解与应用，有效地提高思维的敏捷性、应变性、发散性、创造性等思维品质。一题多变还可以扩大学生知识面，达到举一反三、触类旁通的效果。
例3：如图, △ABC是一块锐角三角形的余料,边长 BC＝120mm,高AD＝80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点在AB、AC上，这个正方形的零件的边长为多少?
分析与简答：该题是相似三角形性质一课中的练习，由△AEH∽△ABC，可以得到比例式
，由于正方形各边相等，故设正方形边长为
，
得
，
，所以正方形的边长为48mm。
变式1： 若把它加工成矩形EFGH，且要求EH=2EF,你能求出该矩形的面积吗？
分析与简答：相似三角形和比例式都是一样的，只是未知数应该换成设EF=x,唯一影响的是EH的长度，可得
，求出x即可。
变式2：怎样剪裁，才能使矩形EFGH的面积最大？
分析与简答：这是一个最值问题，需要与函数知识结合。不妨设一边长为EF=x,另一边EH=y,
, 得
，求出该二次函数最大值即可。
变式3：如左图，在Rt△ABC中，AC=4，BC=3．在Rt△ABC内并排放入（不重叠）n个小正方形纸片，使这些纸片的一边都在AB上，首尾两个正方形各有一个顶点D、E分别在AC、BC上，求小正方形的边长（用n的代数式表示）．
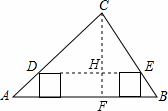
分析与简答：实际上，与变式1类似，我们就可以把下面若干个正方形拼成的图形看成矩形，如右图过C作CF⊥AB，交DE于点H，在Rt△ABC中利用勾股定理易求：
，
，
∵DE∥AB，∴△DEC∽△ABC，
又∵CH⊥DE，CF⊥AB，∴CH：CF=DE：AB，
设小正方形的边长是x，∴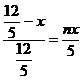
解得：
（四）一题多问，引导思维新拓展
实践证明：处于问题情境中的学生求知欲和好奇心强，他们都主动、积极地参与到学习中去，学习的兴趣高、效率也高。为此，在课堂教学中，我经常会一问再问，引发学生的求知欲和探索问题的好奇心，让我们的学生在不断分析由变式引申出来的各个问题中穿行、碰撞，在碰撞中折射出电火花，产生出磁力线。
在《江苏省初中复习与能力训练》上有一个例题，原题为：
“已知抛物线
（1）若c=-1,求该抛物线与x轴公共点的坐标
（2）若-1<x<1时，抛物线与x轴有且只有一个公共点，求c的取值范围.”
其实该题第一问所有学生都能解决，但是对于第二问往往不会解决或者考虑不全，于是我将其加以变式与追问:
例4：已知抛物线y = 3ax2 + 2bx + c
（1）若a = b = 1，c =－1，求抛物线与x轴公共点的坐标；
（2）若a = b = 1，且当－1＜x＜1时，抛物线与x轴有且只有一个公共点，求c的取值范围.
（3）若a = b = 1，且当－1＜x＜1时，抛物线与x轴有两个公共点，求c的取值范围.
（4）若a = b = 1，且当－1＜x＜1时，抛物线与x轴无公共点，求c的取值范围.
分析与简答：该题应结合二次函数图像解决，同时还渗透了分类讨论的数学思想，另外，对于边界的考虑也是难点。
（1）代入求得与x轴交于（
）（-1，0）
（2），以后几问都是基于这个函数，在列式之前必须先考虑△：△=
①与x轴有且只有一个交点：△=0，
②与x轴有两个交点，但只有一个交点在范围内。当x=-1时，
，当x=1时，
，可得
（3）有两个公共点，首先满足△>0，有
，解得
（4）有两种情况：抛物线与x轴没有交点或者有交点但是交点不在范围内：
①
②当x=1时，.即
综上：
很多学生在解决二次函数题目的时候往往只会套公式求△看交点情况，求顶点解决最值问题，往往不肯动手画个图像去分析。在解决完这一系列问题之后学生不难发现，在解决二次函数问题时，结合它的图像才能把所有情况考虑完整。
二、课后总结
（一）困惑之时，指点迷津
学生遇上不熟悉的题目，往往会不知所措，但是虽然习题呈现形式变化多端，但很多时候是 “形散神不散”。如上面的例2，刚接触第一张图时，看到那么怪异的图形，学生一脸茫然，但是当我有意识地“抱团”呈现一组题，引导学生从“变”的表象中发现“不变”的本质，从“不变”的本质中探求“变”的规律时，学生不仅能自行解决，还会自己画出各种各样新的图形考考同桌。这样既培养了学生灵活多变的思维品质，还能培养其探索精神和创新意识，从而把知识理解能力的提高真正落到实处。
（二）“缺氧”之时，点石成金
在解决例1时，刚开始课堂上只有少数几个学生举手了，但后来当我问到，还有其他解决方法时，好多同学都陆续举手，由解法一得到启示又联想到解法二、三······所有解法“抱团”呈现，提高了学生的兴趣，提高大脑和神经的兴奋度，达到最佳的训练效果。
（三）圆满之时，精益求精
美国著名认知心理学家奥苏伯尔认为，教学的目的是为了知识的迁移，从而塑造良好的认知结构。当设计的问题先易后难、逐级而上，各层次学生在一组题后都能有所提高时，我们还要不失时机地引导学生观察、比较，揭示隐藏在具体的例题、习题中的一般特征，推广为某一类对象的普遍性质，揭示解题规律，提高分析、探索能力和创新能力。
总之，题不在多，选择精而优的例题才是永恒的主题，只有让好题“抱团”呈现，才能帮助学生走出题海，实现变“容量”为“质量”，变“学会”为“会学”，变知识为能力。
【参考文献】：
[1]周海燕.初中数学变式教学浅谈[J].中国校外教育·基教(中旬),2013年11期
[2]席月琴.对一道例题的若干思考[J].初中数学教与学,2012年8月
[3]吴海周.初中数学复习变式训练的实践探究[J].都市家教·下半月 ,2013年第6期
