无锡市张泾中学   严红琴

【摘要】试卷讲评课是数学课堂教学的重要组成部分，是改进教学、提高教学质量的重要途径。本文根据笔者自身多年的教学实践，就提高中学数学试卷讲评的有效性谈谈自己的一些认识和做法，并重点阐述了课堂教师点评的策略，以与同行交流探讨。

【关键词】中学数学  试卷讲评  有效性

在中学教学中，考试是一种重要的教学评价方式，通过考试反馈信息可以对教学进行阶段性总结、反思，从而更有效地处理教学。如何更好地处理考试反馈信息，让考试在教与学两方面体现其价值，其中一个重要环节是试卷讲评。作为师生之间沟通和信息反馈的重要手段，它能起到矫正问题、查缺补漏和巩固基础的作用，从而完善学生的知识体系，提高学生应试技能和学习效果。试卷讲评还可以帮助教师发现自己教学中的不足，进行自我反思，最终达到提高教学质量的目的。因此，如何把数学试卷讲评的有效性落到实处，对学生的数学学习和教师改进教学方法是十分重要的。下面笔者就提高数学试卷讲评课的有效性谈谈自已的体会。

  一、试卷讲评前的准备

高效的讲评要求教师在课前做精心准备。如果教师不能做到心中有数，从头评讲到尾的话，试卷讲评就没有针对性和有效性，学生的激情就不能保持，所以教师要做好有关数据统计，包括测验成绩的各项统计以及各题得分率，提前对试题的难易程度、涉及的知识点、解题的方法技巧、考查的意图、学生错误率较高的题目、有创新的解题方法等都要有一个全面的了解，这样才能对学生整体情况充分掌握并有针对性地点评，针对学生的薄弱环节有的放矢，达到事半功倍的效果。

  二、试卷讲评的方法

试卷讲评有多种形式，归纳起来主要有学生自查、小组互查、学生讲评和教师点评等形式。

  1．学生自查

教师应把要讲评的试卷在作好分析统计后早些发给学生。一些得分率较高的题目可能是学生粗心导致的，这些题可以让学生自行纠错。

  2．小组互查

一些稍有难度的题可以在课堂上适当留一些时间让学生在互动中解决。同学间可以相互讨论、互相帮助，在学生解决问题的同时，帮助同学解决问题的学生也得到了一次锻炼机会。小组合作对培养学生的探究能力和合作精神大有裨益。

  3．学生讲评

对于一些难度较大或学生虽能完成但方法不太恰当的题目，可采用师生共同分析探究的方法。讲评中教师只是引导者，切不可为省事而直接把知识和方法灌输给学生。学生的主体性要体现，教师应多营造学生主动参与讲评的氛围，尽量提供学生自己总结、自行讲评的机会，让拥有新颖解法的同学介绍他们的解法及其思路产生的过程，从而培养学生的表达能力，也让他们体会到成功的喜悦。

  4．教师点评

教师要将试卷中相同或相关内容的题目和解题方法或解题思路相同的题目进行归类讲解，使学生对试卷上同一类问题有一个整体的认识， 使他们对这些知识点的理解更深刻，同时节省时间，提高了课堂效率，能使学生形成系统的知识结构。这样有助于所学知识的深刻理解和巩固。

试卷讲评不单单是对问题答案的分析，而是要以深入拓展地眼光去分析。在讲评课上教师可透过具体问题拓展外延，引导学生开展积极的思维活动，拓展知识，深化技巧，让学生在试题讲评中能有所发现，有所提高。就教师点评的策略来讲，可大致归纳如下：

（1）典型错误，剖析矫正

    例如：下列函数：①y=2x﹣1；②y=﹣；③y=x²+8x﹣2；④y=；⑤y=；⑥y= 中，y是x的反比例函数的有        （填序号）。

   分析： 大多数同学认为这题的答案是②⑤⑥。此题考查反比例函数的概念。反比例函数形如y=,其中k0且k为常数。显然①③④不符合反比例函数的形式，它们不是反比例函数。对于y=，当a0时是反比例函数，但本题中没有此条件，所以它也不是反比例函数，此题的正确答案是②⑤。

对学生典型错误要重点分析出错原因，找到症结所在，然后对症下药。

（2）一题多解，优化解法   

    在教师点评时，教师应积极引导学生通过多种途径、采用多种方法去思考问题，力求从中体现不同的数学知识点，展现知识点之间的联系，渗透数学思想，从而使学生开阔思路，熟练掌握知识点之间的内在联系。

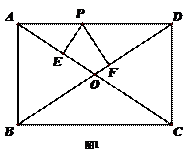
   如图，在矩形ABCD中，AB=6，AD=8，P是AD上一动点，PE⊥AC于E，PF⊥BD于F，则PE+PF=        。

 解法一：（特殊点法）过A作AH⊥BD,在RtABD中，由勾股定理可知BD===10。当P 运动到与点A重合时，点F与点H重合。此时PE的长度为0，PF的长度最大，PF=AH。 =ABAD=BDAH，

∴68=BD10。 ∴ BD=。

解法二：（三角形相似法）在RtACD中，由勾股定理可知 AC==10。

∵PE⊥AC， ∴∠AEP=∠ADC=90°。又∵ ∠PAE=∠CAD，∴AEP∽ADC。  ∴。 设AP的长为x，则PD=8-x。 ∴。 ∴CD=。同理，PF=。 ∴PE+ PF=。

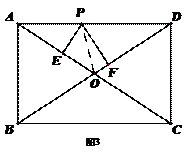
    解法三：（面积法）连接OP。 在矩形ABCD中，OA=OD=5

=， ∴AOPE+ODPF=

∴5PE+5PF=68，∴PE+ PF=。

 以上三种解法分别从特殊点法、相似三角形，和面积法三个角度切入，用到了初中阶段三个重要知识点，通过用不同的方法解决同一道数学题，既可以开拓解题思路，巩固所学知识；又可以激发学生学习数学的兴趣和热情，达到开发潜能，发展智力，提高能力的目的，从而培养学生的探究能力和创新能力。

（3）变式延伸，拓展思维

讲评课的另一个环节是变式拓展。一份试卷所考查的知识点是非常有限的，若在讲评试卷时变换题支或题干，不仅可以融合更多的知识点，还可以让学生从不同的角度明白知识点的内在联系。 此训练层次可浅可深，可根据学生状况和时间适当选择深度、广度。

   例如：如图1，把△ABC的纸片沿着DE折叠，使点A′正好落在线段AC上，此时∠A与∠BDA′有怎样的关系。为什么？

变式1:如果纸片沿DE折叠，使点A′落在四边形BCED的内部，如图2，则∠A和∠BDA′、∠CEA′有怎样的关系？请说明你的理由。

变式2:如果纸片沿DE折叠，使点A′落在四边形BCED的外部，如图3，则此时∠A和∠BDA′、∠